what volume of 1.2 m h2so4 is required to react exactly with 3.5 g of naoh

Affiliate 4. Stoichiometry of Chemical Reactions

4.3 Reaction Stoichiometry

Learning Objectives

Past the end of this section, you will be able to:

• Explain the concept of stoichiometry as it pertains to chemic reactions
• Utilize counterbalanced chemic equations to derive stoichiometric factors relating amounts of reactants and products
• Perform stoichiometric calculations involving mass, moles, and solution molarity

A balanced chemical equation provides a keen bargain of information in a very succinct format. Chemical formulas provide the identities of the reactants and products involved in the chemic change, allowing classification of the reaction. Coefficients provide the relative numbers of these chemic species, allowing a quantitative cess of the relationships between the amounts of substances consumed and produced past the reaction. These quantitative relationships are known as the reaction'due south stoichiometry, a term derived from the Greek words stoicheion (meaning "element") and metron (significant "measure"). In this module, the employ of balanced chemical equations for diverse stoichiometric applications is explored.

The general arroyo to using stoichiometric relationships is similar in concept to the way people become near many common activities. Food preparation, for example, offers an advisable comparison. A recipe for making eight pancakes calls for ane cup pancake mix, [latex]\frac{3}{4}[/latex] cup milk, and ane egg. The "equation" representing the preparation of pancakes per this recipe is

[latex]i \;\text{cup mix} + \frac{3}{4} \;\text{cup milk} + i \;\text{egg} \longrightarrow 8 \;\text{pancakes}[/latex]

If two dozen pancakes are needed for a big family breakfast, the ingredient amounts must be increased proportionally according to the amounts given in the recipe. For case, the number of eggs required to brand 24 pancakes is

[latex]24 \;\rule[0.5ex]{4em}{0.1ex}\hspace{-4em}\text{pancakes} \times \frac{ane \;\text{egg}}{8 \;\rule[0.25ex]{3em}{0.1ex}\hspace{-3em}\text{pancakes}} = 3 \;\text{eggs}[/latex]

Balanced chemic equations are used in much the same fashion to determine the amount of one reactant required to react with a given amount of another reactant, or to yield a given corporeality of product, and so forth. The coefficients in the counterbalanced equation are used to derive stoichiometric factors that let computation of the desired quantity. To illustrate this idea, consider the production of ammonia by reaction of hydrogen and nitrogen:

[latex]\text{N}_2(thousand) + iii\text{H}_2(g) \longrightarrow 2\text{NH}_3(yard)[/latex]

This equation shows ammonia molecules are produced from hydrogen molecules in a 2:iii ratio, and stoichiometric factors may exist derived using whatever amount (number) unit:

[latex]\frac{2 \;\text{NH}_3 \;\text{molecules}}{three \;\text{H}_2 \;\text{molecules}} \;\text{or} \;\frac{2 \;\text{doz NH}_3 \;\text{molecules}}{3 \;\text{doz H}_2 \;\text{molecules}} \;\text{or} \;\frac{two \;\text{mol NH}_3 \;\text{molecules}}{3 \;\text{mol H}_2 \;\text{molecules}}[/latex]

These stoichiometric factors tin exist used to compute the number of ammonia molecules produced from a given number of hydrogen molecules, or the number of hydrogen molecules required to produce a given number of ammonia molecules. Like factors may be derived for whatever pair of substances in whatever chemical equation.

Example 1

Moles of Reactant Required in a Reaction
How many moles of I₂ are required to react with 0.429 mol of Al according to the following equation (see Figure ane)?

[latex]2\text{Al} + three\text{I}_2 \longrightarrow ii\text{AlI}_3[/latex]

Effigy 1. Aluminum and iodine react to produce aluminum iodide. The heat of the reaction vaporizes some of the solid iodine as a purple vapor. (credit: modification of work by Marker Ott)

Solution
Referring to the balanced chemical equation, the stoichiometric factor relating the two substances of interest is [latex]\frac{3 \;\text{mol I}_2}{two \;\text{mol Al}}[/latex]. The molar corporeality of iodine is derived by multiplying the provided tooth amount of aluminum by this factor:

[latex]\begin{assortment}{r @{{}={}} 50} \text{mol I}_2 & 0.429 \;\rule[0.5ex]{3.25em}{0.1ex}\hspace{-3.25em}\text{mol Al} \times \frac{iii \;\text{mol I}_2}{2 \;\rule[0.25ex]{2em}{0.1ex}\hspace{-2em}\text{mol Al}} \\[1em] & 0.644 \;\text{mol I}_2 \cease{array}[/latex]

Check Your Learning
How many moles of Ca(OH)₂ are required to react with 1.36 mol of H₃PO₄ to produce Ca₃(PO₄)₂ according to the equation [latex]3\text{Ca(OH)}_2 + ii\text{H}_3 \text{PO}_4 \longrightarrow \text{Ca}_3 \text{(PO}_4)_2 + half-dozen\text{H}_2 \text{O}[/latex]?

Example 2

Number of Product Molecules Generated by a Reaction
How many carbon dioxide molecules are produced when 0.75 mol of propane is combusted according to this equation?

[latex]\text{C}_3 \text{H}_8 + five\text{O}_2 \longrightarrow 3\text{CO}_2 + four\text{H}_2 \text{O}[/latex]

Solution
The arroyo here is the same as for Example 1, though the absolute number of molecules is requested, not the number of moles of molecules. This volition simply require utilize of the moles-to-numbers conversion gene, Avogadro's number.

The balanced equation shows that carbon dioxide is produced from propane in a 3:one ratio:

[latex]\frac{3 \;\text{mol CO}_2}{1 \;\text{mol C}_3 \text{H}_8}[/latex]

Using this stoichiometric factor, the provided molar amount of propane, and Avogadro'due south number,

[latex]0.75 \;\dominion[0.5ex]{4.5em}{0.1ex}\hspace{-4.5em}\text{mol C}_3 \text{H}_8 \times \frac{iii \;\rule[0.25ex]{3em}{0.1ex}\hspace{-3em} \text{mol CO}_2}{ane \;\rule[0.5ex]{3em}{0.1ex}\hspace{-3em}\text{mol C}_3 \text{H}_8} \times \frac{six.022 \times ten^{23} \;\text{CO}_2 \;\text{molecules}}{\rule[0.25ex]{3em}{0.1ex}\hspace{-3em} \text{mol CO}_2} = 1.4 \times 10^{24} \text{CO}_2 \;\text{molecules}[/latex]

Check Your Learning
How many NH₃ molecules are produced past the reaction of iv.0 mol of Ca(OH)₂ according to the following equation:

[latex](\text{NH}_4)_2 \text{And then}_4 + \text{Ca(OH)}_2 \longrightarrow 2\text{NH}_3 + \text{CaSO}_4 + two\text{H}_2 \text{O}[/latex]

Answer:

iv.8 × x²⁴ NH₃ molecules

These examples illustrate the ease with which the amounts of substances involved in a chemical reaction of known stoichiometry may be related. Directly measuring numbers of atoms and molecules is, however, non an easy job, and the applied application of stoichiometry requires that we employ the more readily measured property of mass.

Example 3

Relating Masses of Reactants and Products
What mass of sodium hydroxide, NaOH, would be required to produce 16 one thousand of the antacid milk of magnesia [magnesium hydroxide, Mg(OH)_two] by the following reaction?

[latex]\text{MgCl}_2(aq) + 2\text{NaOH}(aq) \longrightarrow \text{Mg(OH)}_2(s) + \text{NaCl}(aq)[/latex]

Solution
The approach used previously in Instance 1 and Example 2 is likewise used here; that is, we must derive an appropriate stoichiometric factor from the counterbalanced chemical equation and use it to relate the amounts of the two substances of interest. In this case, even so, masses (not molar amounts) are provided and requested, and then boosted steps of the sort learned in the previous chapter are required. The calculations required are outlined in this flowchart:

[latex]16 \;\rule[0.5ex]{5em}{0.1ex}\hspace{-5em}\text{1000 Mg(OH)}_2 \times \frac{1 \;\dominion[0.25ex]{4.75em}{0.1ex}\hspace{-4.75em}\text{mol Mg(OH)}_2}{58.three \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-three.5em}\text{m Mg(OH)}_2} \times \frac{ii \;\rule[0.25ex]{iii.5em}{0.1ex}\hspace{-iii.5em}\text{mol NaOH}}{i \;\rule[0.25ex]{4.5em}{0.1ex}\hspace{-four.5em}\text{mol Mg(OH)}_2} \times \frac{forty.0 \;\text{grand NaOH}}{1 \;\rule[0.25ex]{3.25em}{0.1ex}\hspace{-3.25em}\text{mol NaOH}} = 22 \;\text{g NaOH}[/latex]

Check Your Learning
What mass of gallium oxide, Ga₂O₃, tin be prepared from 29.0 g of gallium metallic? The equation for the reaction is [latex]iv \text{Ga} + 3\text{O}_2 \longrightarrow 2\text{Ga}_2 \text{O}_3.[/latex]

Example four

Relating Masses of Reactants
What mass of oxygen gas, O_ii, from the air is consumed in the combustion of 702 g of octane, C₈H₁₈, ane of the main components of gasoline?

[latex]2\text{C}_8 \text{H}_{18} + 25\text{O}_2 \longrightarrow sixteen\text{CO}_2 + eighteen\text{H}_2 \text{O}[/latex]

Solution
The approach required here is the same every bit for the Case 3, differing but in that the provided and requested masses are both for reactant species.

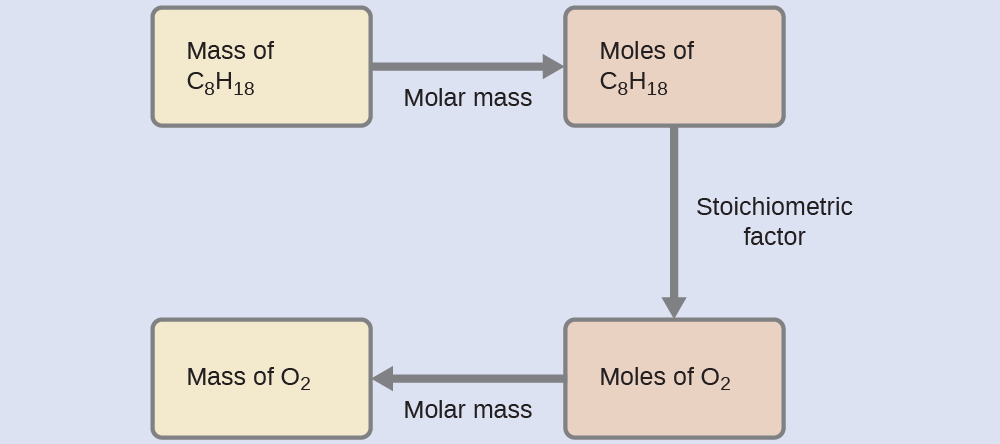
[latex]702 \;\dominion[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{g C}_8 \text{H}_{18} \times \frac{one \;\rule[0.25ex]{three.5em}{0.1ex}\hspace{-three.5em}\text{mol C}_8 \text{H}_{18}}{114.23 \;\rule[0.25ex]{2.75em}{0.1ex}\hspace{-two.75em}\text{thousand C}_8 \text{H}_{18}} \times \frac{25 \;\rule[0.25ex]{2.5em}{0.1ex}\hspace{-2.5em}\text{mol O}_2}{2 \;\rule[0.25ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol C}_8 \text{H}_{xviii}} \times \frac{32.00 \;\text{k O}_2}{\rule[0.25ex]{2.5em}{0.1ex}\hspace{-2.5em}\text{mol O}_2} = 2.46 \times 10^iii \;\text{g O}_2[/latex]

Cheque Your Learning
What mass of CO is required to react with 25.13 chiliad of Fe_twoO₃ according to the equation
[latex]\text{Atomic number 26}_2 \text{O}_3 + 3\text{CO} \longrightarrow ii\text{Atomic number 26} + three\text{CO}_2[/latex]

These examples illustrate just a few instances of reaction stoichiometry calculations. Numerous variations on the beginning and ending computational steps are possible depending upon what particular quantities are provided and sought (volumes, solution concentrations, and so forth). Regardless of the details, all these calculations share a common essential component: the use of stoichiometric factors derived from balanced chemical equations. Figure 2 provides a general outline of the various computational steps associated with many reaction stoichiometry calculations.

Effigy two. The flowchart depicts the diverse computational steps involved in most reaction stoichiometry calculations.

Airbags

Airbags (Effigy 3) are a condom feature provided in most automobiles since the 1990s. The effective functioning of an airbag requires that it be quickly inflated with an appropriate corporeality (volume) of gas when the vehicle is involved in a collision. This requirement is satisfied in many automotive airbag systems through use of explosive chemical reactions, ane common choice being the decomposition of sodium azide, NaN₃. When sensors in the vehicle detect a collision, an electrical electric current is passed through a carefully measured amount of NaN₃ to initiate its decomposition:

[latex]ii \text{NaN}_3(s) \longrightarrow iii\text{N}_2(g) + two\text{Na}(south)[/latex]

This reaction is very rapid, generating gaseous nitrogen that can deploy and fully inflate a typical airbag in a fraction of a second (~0.03–0.one due south). Amidst many engineering considerations, the amount of sodium azide used must exist appropriate for generating plenty nitrogen gas to fully inflate the air bag and ensure its proper function. For case, a minor mass (~100 g) of NaN₃ will generate approximately fifty L of N₂.

Figure 3. Airbags deploy upon touch on to minimize serious injuries to passengers. (credit: Jon Seidman)

Key Concepts and Summary

A counterbalanced chemical equation may be used to describe a reaction's stoichiometry (the relationships betwixt amounts of reactants and products). Coefficients from the equation are used to derive stoichiometric factors that after may be used for computations relating reactant and product masses, molar amounts, and other quantitative properties.

Chemistry Cease of Chapter Exercises

1. Write the balanced equation, then outline the steps necessary to determine the data requested in each of the post-obit:

   (a) The number of moles and the mass of chlorine, Cl_two, required to react with 10.0 thousand of sodium metal, Na, to produce sodium chloride, NaCl.

   (b) The number of moles and the mass of oxygen formed by the decomposition of 1.252 grand of mercury(Two) oxide.

   (c) The number of moles and the mass of sodium nitrate, NaNO₃, required to produce 128 g of oxygen. (NaNO₂ is the other product.)

   (d) The number of moles and the mass of carbon dioxide formed past the combustion of 20.0 kg of carbon in an excess of oxygen.

   (e) The number of moles and the mass of copper(2) carbonate needed to produce one.500 kg of copper(2) oxide. (CO₂ is the other product.)

   (f)
   

2. Decide the number of moles and the mass requested for each reaction in Chemistry Stop of Chapter Practise 1.
3. Write the balanced equation, so outline the steps necessary to determine the information requested in each of the following:

   (a) The number of moles and the mass of Mg required to react with 5.00 g of HCl and produce MgCl₂ and H₂.

   (b) The number of moles and the mass of oxygen formed by the decomposition of i.252 g of silver(I) oxide.

   (c) The number of moles and the mass of magnesium carbonate, MgCO_three, required to produce 283 g of carbon dioxide. (MgO is the other product.)

   (d) The number of moles and the mass of h2o formed past the combustion of 20.0 kg of acetylene, C₂H₂, in an backlog of oxygen.

   (due east) The number of moles and the mass of barium peroxide, BaO₂, needed to produce ii.500 kg of barium oxide, BaO (O₂ is the other product.)

   (f)
   

4. Make up one's mind the number of moles and the mass requested for each reaction in Chemistry Cease of Chapter Exercise iii.
5. H₂ is produced by the reaction of 118.5 mL of a 0.8775-M solution of H_iiiPO₄ according to the following equation: [latex]2\text{Cr} + two\text{H}_3 \text{PO}_4 \longrightarrow three\text{H}_2 + 2\text{CrPO}_4[/latex].

   (a) Outline the steps necessary to make up one's mind the number of moles and mass of H₂.

   (b) Perform the calculations outlined.

6. Gallium chloride is formed by the reaction of two.vi L of a 1.44 Chiliad solution of HCl according to the post-obit equation: [latex]ii\text{Ga} + 6\text{HCl} \longrightarrow 2\text{GaCl}_3 + 3\text{H}_2[/latex].

   (a) Outline the steps necessary to determine the number of moles and mass of gallium chloride.

   (b) Perform the calculations outlined.

7. I₂ is produced by the reaction of 0.4235 mol of CuCl₂ according to the following equation: [latex]two\text{CuCl}_2 + iv\text{KI} \longrightarrow two\text{CuI} + 4\text{KCl} + \text{I}_2[/latex].

   (a) How many molecules of I₂ are produced?

   (b) What mass of I_two is produced?

8. Silver is often extracted from ores such as K[Ag(CN)₂] and and so recovered past the reaction
   [latex]2 \text{Thousand} [\text{Ag(CN)}_2](aq) + \text{Zn}(s) \longrightarrow 2\text{Ag}(s) + \text{Zn(CN)}_2(aq) + 2\text{KCN}(aq)[/latex]

   (a) How many molecules of Zn(CN)_ii are produced by the reaction of 35.27 g of One thousand[Ag(CN)₂]?

   (b) What mass of Zn(CN)₂ is produced?

9. What mass of silver oxide, Ag_twoO, is required to produce 25.0 g of silverish sulfadiazine, AgC₁₀H₉N_fourAnd then₂, from the reaction of silver oxide and sulfadiazine?
   [latex]2\text{C}_{10} \text{H}_{10} \text{Due north}_4 \text{So}_2 + \text{Ag}_2 \text{O} \longrightarrow ii\text{Ag} \text{C}_{10} \text{H}_{9} \text{North}_4 \text{SO}_2 + \text{H}_2 \text{O}[/latex]
10. Carborundum is silicon carbide, SiC, a very hard fabric used equally an abrasive on sandpaper and in other applications. It is prepared by the reaction of pure sand, SiO₂, with carbon at loftier temperature. Carbon monoxide, CO, is the other product of this reaction. Write the balanced equation for the reaction, and summate how much SiO₂ is required to produce three.00 kg of SiC.
11. Automotive air numberless inflate when a sample of sodium azide, NaN₃, is very rapidly decomposed.
    [latex]2\text{NaN}_3(southward) \longrightarrow 2\text{Na}(s) + 3\text{North}_2(g)[/latex]

    What mass of sodium azide is required to produce two.half-dozen ft^three (73.6 L) of nitrogen gas with a density of 1.25 g/L?

12. Urea, CO(NH₂)₂, is manufactured on a large calibration for use in producing urea-formaldehyde plastics and as a fertilizer. What is the maximum mass of urea that can be manufactured from the CO₂ produced by combustion of 1.00×103kg1.00×103kg of carbon followed by the reaction?
    [latex]\text{CO}_2(g) + ii\text{NH}_3(g) \longrightarrow {\text{CO(NH}_2})_2(south) + \text{H}_2 \text{O}(fifty)[/latex]
13. In an accident, a solution containing ii.v kg of nitric acid was spilled. Two kilograms of Na_iiCO₃ was quickly spread on the area and CO_ii was released by the reaction. Was sufficient Na₂CO_iii used to neutralize all of the acid?
14. A compact machine gets 37.5 miles per gallon on the highway. If gasoline contains 84.2% carbon past mass and has a density of 0.8205 g/mL, make up one's mind the mass of carbon dioxide produced during a 500-mile trip (three.785 liters per gallon).
15. What volume of 0.750 1000 hydrochloric acrid solution can exist prepared from the HCl produced by the reaction of 25.0 k of NaCl with backlog sulfuric acid?[latex]\text{NaCl}(s) + \text{H}_2 \text{And so}_4(l) \longrightarrow \text{HCl}(g) + \text{NaHSO}_4(s)[/latex]
16. What volume of a 0.2089 Thou KI solution contains enough KI to react exactly with the Cu(NO_three)₂ in 43.88 mL of a 0.3842 1000 solution of Cu(NO_iii)₂?[latex]2 \text{Cu(NO}_3)_2 + 4\text{KI} \longrightarrow two\text{CuI} + \text{I}_2 + iv{\text{KNO}_3}[/latex]
17. A mordant is a substance that combines with a dye to produce a stable fixed color in a dyed fabric. Calcium acetate is used as a mordant. It is prepared past the reaction of acetic acid with calcium hydroxide.[latex]ii\text{CH}_3 \text{CO}_2 \text{H} + \text{Ca(OH)}_2 \longrightarrow \text{Ca(CH}_3 \text{CO}_2)_2 + 2\text{H}_2 \text{O}[/latex]

    What mass of Ca(OH)_two is required to react with the acetic acid in 25.0 mL of a solution having a density of 1.065 g/mL and containing 58.0% acetic acid by mass?

18. The toxic pigment chosen white lead, Pb₃(OH)₂(CO₃)₂, has been replaced in white paints past rutile, TiO_ii. How much rutile (g) can exist prepared from 379 k of an ore that contains 88.3% ilmenite (FeTiO₃) by mass?[latex]2\text{FeTiO}_3 + four\text{HCl} + \text{Cl}_2 \longrightarrow 2\text{FeCl}_3 + 2\text{TiO}_2 + two\text{H}_2 \text{O}[/latex]

Glossary

stoichiometric cistron

ratio of coefficients in a balanced chemical equation, used in computations relating amounts of reactants and products

stoichiometry

relationships between the amounts of reactants and products of a chemical reaction

Solutions

Answers to Chemistry Finish of Affiliate Exercises

2. (a) 0.435 mol Na, 0.217 mol Cl₂, xv.4 g Cl₂; (b) 0.005780 mol HgO, 2.890 × ten^−three mol O_ii, 9.248 × 10⁻² yard O₂; (c) 8.00 mol NaNO₃, 6.8 × 10² g NaNO₃; (d) 1665 mol CO₂, 73.iii kg CO_ii; (eastward) xviii.86 mol CuO, 2.330 kg CuCO_three; (f) 0.4580 mol C₂H_fourBr_ii, 86.05 1000 C_iiH₄Br₂

4. (a) 0.0686 mol Mg, 1.67 g Mg; (b) 2.701 × 10⁻³ mol O₂, 0.08644 m O₂; (c) 6.43 mol MgCO_iii, 542 k MgCO₃ (d) 713 mol H_twoO, 12.viii kg H₂O; (e) xvi.31 mol BaO₂, 2762 grand BaO₂; (f) 0.207 mol C_iiH₄, 5.81 1000 C_iiH_iv

half-dozen. (a) [latex]\text{volume HCl solution} \longrightarrow \text{mol HCl} \longrightarrow \text{mol GaCl}_3[/latex]; (b) i.25 mol GaCl₃, 2.2 × x² thou GaCl₃

8. (a) v.337 × x²² molecules; (b) x.41 k Zn(CN)₂

10. [latex]\text{SiO}_2 + 3\text{C} \longrightarrow \text{SiC} + 2\text{CO}[/latex], 4.l kg SiO₂

12. 5.00 × 10^three kg

xiv. 1.28 × 10⁵ k CO₂

16. 161.twoscore mL KI solution

18. 176 thousand TiO_ii

woodruffalligns.blogspot.com

Source: https://opentextbc.ca/chemistry/chapter/4-3-reaction-stoichiometry/

Share this post